1388. Petrol stations
There are n cities in the country, some of which are connected
by roads. To travel along one road, one tank of gasoline is required. In each
city, the cost of a full tank of gasoline is different. Your task is to get
from the first city to the n-th city with minimum expenses.
Input. The first line
contains the number of cities n (1 ≤ n ≤ 100). The
second line contains n numbers, where the i-th
number represents the cost of gasoline in the i-th city (all
numbers are integers from 0 to 100). The third line contains the
number of roads m in the country, followed by the description
of the roads. Each road is represented by two numbers – the numbers of the
cities it connects. All roads are bidirectional (that is, you can travel in
both directions), there is at most one road between any two cities, and there
are no roads that lead from a city to itself.
Output. Print a single
integer – the minimum cost of the route, or -1 if it is impossible to reach
the n-th city.
|
Sample
input 1 |
Sample
output 1 |
|
4 1 10 2 15 4 1 2 1 3 4 2
4 3 |
3 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
4 1 10 2 15 0 |
-1 |
SOLUTION
graphs – Dijkstra
Algorithm analysis
Let cost[i] be the cost of gasoline in the i-th city. For
each pair of cities i and j, add a directed edge from i to j
with weight cost[i], as well as a directed edge from j to i
with weight cost[j].
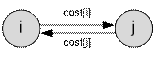
To solve the problem, find
the minimum cost path from city 1 to city n.
Example
Let’s construct the
graph given in the first
example.
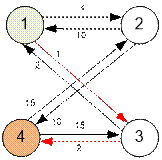
The minimum cost route
from vertex 1 to vertex 4 is: 1 → 3 → 4. Its cost is 1 + 2 = 3.
Algorithm realization
Store the graph
in an adjacency
matrix g. The current shortest distances from the starting vertex 1 to the other vertices are stored in an array d. The array cost holds the gasoline cost in
each city.
#define MAX 110
#define INF 0x3F3F3F3F
int g[MAX][MAX],
used[MAX], d[MAX], cost[MAX];
Read the number
of cities n and the gasoline cost in each of them.
scanf("%d",&n);
for(i = 1; i <= n; i++)
scanf("%d",&cost[i]);
Construct a graph representing the costs of traveling between cities.
memset(mas,0x3F,sizeof(mas));
memset(used,0,sizeof(used));
scanf("%d",&m);
for(i = 1; i <= m; i++)
{
scanf("%d
%d",&a,&b);
g[a][b] = cost[a];
g[b][a] = cost[b];
}
Initialize the shortest distances from the first vertex to the other vertices.
memset(d,0x3F,sizeof(d));
d[1] = 0;
Start the loop of Dijkstra’s algorithm. In
each iteration find the vertex w with the minimum distance mind from the starting vertex.
for(i = 1; i < n; i++)
{
mind = INF; w = -1;
for(j = 1; j
<= n; j++)
if
(!used[j] && d[j] < mind) {mind = d[j]; w = j;}
If it turns out that w = -1, then the desired path does
not exist, and
we exit the loop.
if (w < 0)
break;
Relax all edges originating from vertex w.
for (j =
1; j <= n; j++)
if (!used[j]) d[j] =
min(d[j], d[w] + g[w][j]);
The shortest distance to vertex w is computed.
used[w] = 1;
}
Print the answer based
on the value of dist[n]. If it is infinity, then there is no path to vertex n.
Otherwise, print the shortest distance found.
if (d[n] == INF) printf("-1\n");
else printf("%d\n",d[n]);
Java
realization
import java.util.*;
public class Main
{
static final int INFINITY = 2000000000;
static int g[][], used[], dist[], cost[];
static void Relax(int i, int j)
{
if (dist[i] + g[i][j] < dist[j])
dist[j] = dist[i] + g[i][j];
}
public static void main(String[] args)
{
Scanner
con = new Scanner(System.in);
int n = con.nextInt();
g = new int[n+1][n+1];
for (int[] row: g) Arrays.fill(row, INFINITY);
cost = new int[n+1];
for (int i = 1; i <= n; i++)
cost[i] = con.nextInt();
used = new int[n+1]; Arrays.fill(used, 0);
dist = new int[n+1]; Arrays.fill(dist, INFINITY);
dist[1] = 0;
int m = con.nextInt();
for (int i = 1; i <= m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g[a][b] = cost[a];
g[b][a] = cost[b];
}
for (int i = 1; i < n; i++)
{
// find vertex w with minimum d[w] among not used vertices
int min = INFINITY, v = -1;
for (int j = 1; j <= n; j++)
if (used[j] == 0 && dist[j] < min) { min = dist[j]; v = j; }
// no more vertices to add
if (v < 0) break;
// relax all edges outgoing from v
// process edge v -> j
for (int j = 1; j <= n; j++)
if (used[j] == 0 && g[v][j] != -1) Relax(v, j);
// shortest distance to v is found
used[v] = 1;
}
if (dist[n] == INFINITY) System.out.println(-1);
else System.out.println(dist[n]);
con.close();
}
}